📝题目
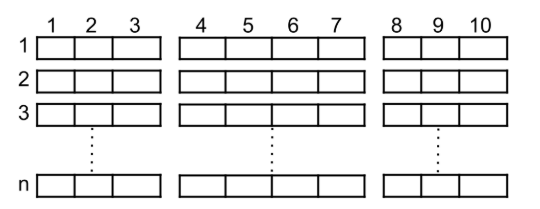
1 | 如图一所示,电影院的观影厅中有 n 行座位,行编号从 1 到 n ,且每一行内总共有 10 个座位,列编号从 1 到 10 。 |
📝思路
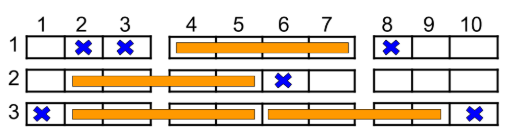
对于一个家庭而言,只有以下三种给他们安排座位的方法:
- 安排位置 2,3,4,5;
- 安排位置 4,5,6,7;
- 安排位置 6,7,8,9。
因此每一排的位置 1 和位置 10 都是没有意义的,即使被预约了也对答案没有任何影响,所以,忽略所有在位置 1 和位置 10 的预约。同时可以发现,如果一排位置(不含位置 1 和位置 10 ,下同)没有被预约,那么恰好可以安排给两个家庭;如果一排位置被预约了至少一个座位,那么最多只能安排给一个家庭了。
对于只能安排一个家庭的情况,有两种方法计算。
方法一:查找。即利用STL自定义的函数暴力查找。
方法二:位运算。
用哈希表来存储每一排以及它们的二进制数。对于哈希映射中的每个键值对,键表示电影院中的一排,值表示这一排对应的二进制数。如果某一排没有任何位置被预约(例如上面的第三排),那么这一排一定可以安排给两个家庭,因此可以不必将这个键值对存放在哈希映射中。也就是说,只有某一排的某一座位被预约了,才将这一排放入哈希映射。
在处理完了所有的预约之后,遍历哈希映射。对于一个键值对 (row,bitmask),如何知道 row 这一排可以安排给几个家庭呢?根据之前的分析,被存储在哈希映射中的这些排最多只能安排给一个家庭,那么对于三种安排座位的方法:
- 对于安排位置 2,3,4,5,如果 bitmask 中第 0,1,2,3 个二进制位均为 0,那么就可以安排给一个家庭;也就是说,bitmask 和 (11110000)2 的按位或值保持为 (11110000)2 不变;
- 对于安排位置 4,5,6,7,如果 bitmask 中第 2,3,4,5 个二进制位均为 0,那么就可以安排给一个家庭;也就是说,bitmask 和 (11000011)2 的按位或值保持为 (11000011)2 不变;
- 对于安排位置 6,7,8,9,如果 bitmask 中第 4,5,6,7 个二进制位均为 0,那么就可以安排给一个家庭;也就是说,bitmask 和 (00001111)2 的按位或值保持为 (00001111)2 不变;
这样以来,我们只需要将 bitmask 分别与 (11110000)2、 (11000011)2 和 (00001111)2进行按位或运算,如果其中有一个在运算后保持不变,那么 row 这一排就可以安排给一个家庭。
🐣:auto冒号遍历为 C++11 新特性,参见 C++11 auto冒号遍历、C++之auto使用;温习一下左移/右移运算符。
📝题解
1 | //想法一 |
1 | //想法二 |
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.