LeetCode-983 最低票价

📝题目

在一个火车旅行很受欢迎的国度，你提前一年计划了一些火车旅行。在接下来的一年里，你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。

火车票有三种不同的销售方式：

· 一张为期一天的通行证售价为 costs[0] 美元；
· 一张为期七天的通行证售价为 costs[1] 美元；
· 一张为期三十天的通行证售价为 costs[2] 美元。

通行证允许数天无限制的旅行。 例如，如果我们在第 2 天获得一张为期 7 天的通行证，那么我们可以连着旅行 7 天：第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。

返回你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费。

示例 1：

输入：days = [1,4,6,7,8,20], costs = [2,7,15]
输出：11
解释： 
例如，这里有一种购买通行证的方法，可以让你完成你的旅行计划：
在第 1 天，你花了 costs[0] = $2 买了一张为期 1 天的通行证，它将在第 1 天生效。
在第 3 天，你花了 costs[1] = $7 买了一张为期 7 天的通行证，它将在第 3, 4, ..., 9 天生效。
在第 20 天，你花了 costs[0] = $2 买了一张为期 1 天的通行证，它将在第 20 天生效。
你总共花了 $11，并完成了你计划的每一天旅行。

示例 2：

输入：days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
输出：17
解释：
例如，这里有一种购买通行证的方法，可以让你完成你的旅行计划： 
在第 1 天，你花了 costs[2] = $15 买了一张为期 30 天的通行证，它将在第 1, 2, ..., 30 天生效。
在第 31 天，你花了 costs[0] = $2 买了一张为期 1 天的通行证，它将在第 31 天生效。 
你总共花了 $17，并完成了你计划的每一天旅行。

限制：
· 1 <= days.length <= 365
· 1 <= days[i] <= 365
· days 按顺序严格递增
· costs.length == 3
· 1 <= costs[i] <= 1000

📝思路

主干思路：

• 今天不需要出门，不用买票
• 今天如果要出门，需要买几天？
  • 看往后几天（最多30天内）要不要出门
    • 30天内都没有要出行的，那只买今天就好
    • 有要出门的（不同决策）
      • 这次 和 后面几次 分开买更省
      • 这次 和 后面几次 一起买更省

上述思路显而易见，最关键在于：「今天买多少，得看后几天怎么安排」，即「前面依赖后面」——从后向前来买。

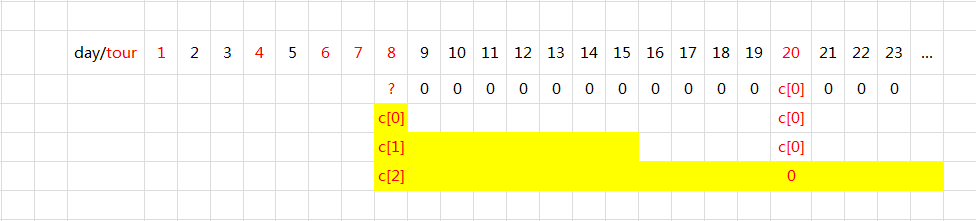
如图所示，例如：$days = [1,4,6,7,8,20]$

• 第 21 及以后的日子都不需要出门，不用买票
• 第 20 需要出门，需要买几天？
  • 不考虑 20 之前要不要出门，否则与思路相违背
  • 第 20 之后没有出门日，故买「一天」的 costs[0] 最省钱。
• 第 9 - 19 不需要出门，则不用买
• 第 8 需要出门，需要买几天？
  • 往后（只需看往后30天）有出门的需求
    • 决策1：买一天期，后面的不包
    • 决策2：买七天期，包到第 8 + 7 - 1 天，第 8 + 7 天往后的不包
    • 决策3：买三十天期，包到第 8 + 30 - 1 天，第 8 + 30 天往后的不包
      • 可见，决策3 包三十天期的话，第 20 可不用花钱

• …
• 抽象，定义状态：dp[i] 为第 i 天开始，累计所需最小费用

  dp[i] = min(决策1, 决策2, 决策3);    
        = min(c[0] + 1天后不包, c[1] + 7天后不包, c[2] + 30天不包);
        = min(c[0] + dp[i + 1], c[1] + dp[i + 7], c[2] + dp[i + 30]);

📝题解

int mincostTickets(vector<int>& days, vector<int>& costs) {
    int len = days.size();
    int dp[400] = {0};

    for (int d = days[len-1], i = len-1; d >= days[0]; --d){
        if (d == days[i]){
            dp[d] = min(costs[0]+dp[d+1], costs[1]+dp[d+7]);
            dp[d] = min(costs[2]+dp[d+30], dp[d]);
            --i;
        }
        else dp[d] = dp[d+1];
    }
    return dp[days[0]];
}